Advertisements
Advertisements
Question
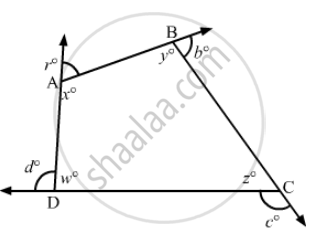
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
Solution
\[\text{ The sides of the quadrilateral ABCD are produced in order (according to figure) . } \]
\[\text{ Now, we need to find the sum of the exterior angles } . \]
\[\text{ Since the angles made on the same side of straight line are } 180 °, \text{ i . e . , linear pair, we have: } \]
\[a + x + b + y + c + z + w + d = 180° + 180° + 180° + 180°= 720° \]
\[OR \]
\[\text{ Sum of the interior angles + sum of exterior the angles } = 180 ° \times 4 = 720° \]
\[ \text{ Since the sum of the interior angles of a quadrilateral is } 360° , \text{ we have } : \]
\[w + x + y + z = 360° \]
\[ \text{ Substituing the value, we get } : \]
\[a + b + c + d = 360° \]
\[ \therefore \text{ Sum of the exterior angles } = 360 ° \]
APPEARS IN
RELATED QUESTIONS
What is the sum of the measures of the angels of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Complete of the following, so as to make a true statement:
The sum of the angles of a quiadrilateral is .... right angles.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
Write two conditions that will make the adjoining figure a square.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
Which of the following is not true for a parallelogram?
In figure, ∠XYZ cannot be written as ______.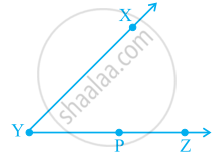
Using the information given, name the right angles in part of figure:
AE ⊥ CE
