Advertisements
Advertisements
Question
In Fig. 16.20, find the measure of ∠MPN.
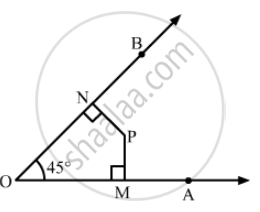
Solution
\[\text{ Since the sum of all the angles of a quadrilateral is } 360°, \text{ we have } : \]
\[45° + 90° + 90° + ∠MPN = 360° \]
\[ \Rightarrow 225° + ∠MPN = 360°\]
\[ \therefore ∠MPN = 135° \]
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Sides.
Complete of the following, so as to make a true statement:
The number of pairs of opposite angles of a quadrilateral is .......
Complete of the following, so as to make a true statement:
The sum of the angles of a quiadrilateral is .... right angles.
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles
In quadrilateral WXYZ, the pairs of opposite angles are ______.
Number of angles less than 180° in figure is ______ and their names are ______.
Using the information given, name the right angles in part of figure:
RS ⊥ RW
