Advertisements
Advertisements
Question
What is the sum of the measures of the angels of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Solution
The sum of the measures of the angles of a convex quadrilateral is 360° as a convex quadrilateral is made of two triangles.

Here, ABCD is a convex quadrilateral, made of two triangles ΔABD and ΔBCD. Therefore, the sum of all the interior angles of this quadrilateral will be same as the sum of all the interior angles of these two triangles i.e., 180º + 180º = 360º
Yes, this property also holds true for a quadrilateral which is not convex. This is because any quadrilateral can be divided into two triangles.
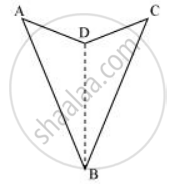
Here again, ABCD is a concave quadrilateral, made of two triangles ΔABD and ΔBCD. Therefore, sum of all the interior angles of this quadrilateral will also be 180º + 180º = 360º
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Diagonals .
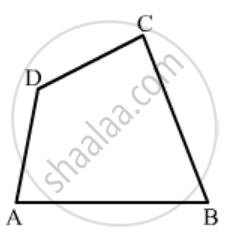
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite sides are there?
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
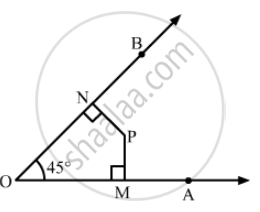
In Fig. 16.20, find the measure of ∠MPN.
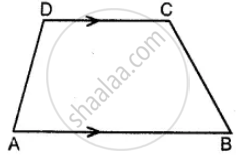
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is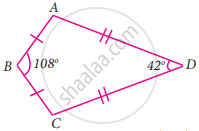
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
In the given figure.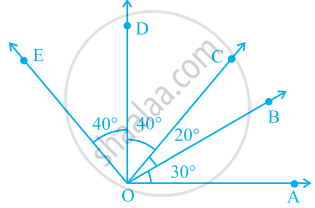
∠COA is a/an ______ angle
