Advertisements
Advertisements
Question
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Solution
\[\text{ Let x be the the fourth angle } . \]
\[\text{ Since, the sum of all the angles of a quadrilateral is } 360°, \text{ we have: } \]
\[110°+ 50° + 40° + x = 360° \]
\[ \Rightarrow 200° + x = 360°\]
\[ \Rightarrow x = 160° \]
\[ \therefore \text{ The fourth angle is 160 } ° .\]
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Exterior .
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Angle A of an isosceles trapezium ABCD is 115°; find the angles B, C and D.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
Observe the figure below and find out their name.
The angles of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
Construct a quadrilateral NEWS in which NE = 7 cm, EW = 6 cm, ∠N = 60°, ∠E = 110° and ∠S = 85°.
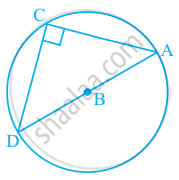
Using the information given, name the right angles in part of figure:
AC ⊥ CD