Advertisements
Advertisements
Question
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
Solution 1
Given, Angles of a quadrilateral are in the ratio 2 : 3 : 2 : 3
i.e. A : B : C : D are in the ratio
2 : 3 : 2 : 3
To prove: Quadrilateral ABCD is a parallelogram
Proof: Let us take ∠A = 2x, ∠B = 3x, ∠C = 2x and ∠D = 3x
We know, that the sum of interior angles of a quadrilateral = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 2x + 3x + 2x + 3x = 360°
⇒ 10x = 360°
⇒ x = `360^circ/10 = 36^circ`
∴ ∠A = ∠C = 2x = 2 × 360° = 72°
∠B = ∠D = 3x = 3 × 36° = 360°
Now, A quadrilateral ABCD is considered as a parallelogram.
(i) When opposite angles are equal,
i.e. ∠A = ∠C = 72° and ∠B = ∠D = 108°
(ii) When adjacent angles are supplementary
i.e. ∠A + ∠B = 180°
and ∠C = ∠D = 180°
⇒ 72° + 108° and 72° + 108° = 180°
⇒ 180° = 180° and 180° = 180°
Since quadrilateral ABCD fulfills the conditions.
∴ Quadrilateral ABCD is a parallelogram.
Solution 2
The sum of all angles in a quadrilateral is 360∘. Let the angles of the quadrilateral be 2x, 3x, 2x, and 3x.
Using the sum of the angles:
2x + 3x + 2x + 3x = 360∘.
Simplify: 10x = 360∘
x = 36∘
Substitute x = 36∘ into the expressions for the angles:
- 2x = 2 × 36 = 72∘
- 3x = 3 × 36 = 108∘
Thus, the angles are: 72∘, 108∘, 72∘, 108∘
In a parallelogram, opposite angles are equal. Here:
- One pair of opposite angles: 72∘, 72∘,
- Another pair of opposite angles: 108∘, 108∘
Since opposite angles are equal, the quadrilateral satisfies the property of a parallelogram.
The given quadrilateral is a parallelogram because its opposite angles are equal
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
The sum of the angles of a quadrilateral is ......
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = x° and ∠D = (3x – 20)°; find the value of x.
Write, giving reason, the name of the figure drawn alongside. Under what condition will this figure be a square.
Observe the figure below and find out their name.
Find the angles of a pentagon which are in the ratio 4: 4: 6: 7: 6.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
Calculate the measure of each angle of a nonagon.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form ______.
Which of the following is not true for a parallelogram?
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is ______.
A quadrilateral can have all four angles as obtuse.
Measures of the two angles between hour and minute hands of a clock at 9 O’ clock are ______.
Using the information given, name the right angles in part of figure:
AC ⊥ BD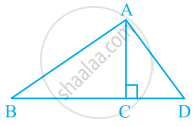
Using the information given, name the right angles in part of figure:
RS ⊥ RW
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?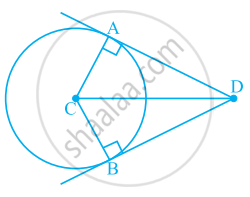
Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Investigate :
Use strips and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral. Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilaterals?
