Advertisements
Advertisements
Question
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is ______.
Options
∠DAE = ∠EFC
AE = EF
DE = EF
∠ADE = ∠ECF
Solution
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is DE = EF.
Explanation:
We have produced DE to F such that
DE = EF ...(1)
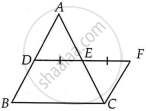
In ΔADE and ΔCFE,
AE = CE ...[Since, E is the mid-point of AC]
∠AED = ∠CEF ...[Vertically opposite angles]
DE = FE ...[By (1)]
∴ ΔADE ≅ ΔCFE ...[By SAS congruency]
∴ AD = CF and ∠ADE = ∠CFE ...[By C.P.C.T.]
This shows that alternate interior angles are equal.
Thus, AD || CF
Therefore, the additional information which we need is DE = EF
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Diagonals .
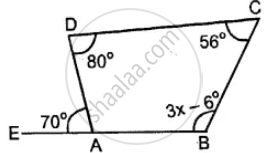
Use the information given in the following figure to find the value of x.
The angles A, B, C and D of a trapezium ABCD are in the ratio 3: 4: 5: 6. Le. ∠A : ∠B : ∠C : ∠D = 3:4: 5 : 6. Find all the angles of the trapezium. Also, name the two sides of this trapezium which are parallel to each other. Give reason for your answer.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
Observe the figure below and find out their name.
In quadrilateral ROPE, the pairs of adjacent angles are ______.
In given figure, What is AC – EC?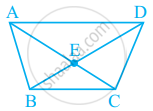
In given figure, What is BD – BE?
Using the information given, name the right angles in part of figure:
AE ⊥ CE
