Advertisements
Advertisements
Question
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
Solution
∵ The diagonals of an isosceles trapezium are of equal length

∴ 3x – 8 = x
⇒ 3x – x = 8 cm
⇒ 2x = 8 cm
⇒ x = 4 cm
∴ The value of x is 4 cm
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
The sum of the angles of a quadrilateral is ......
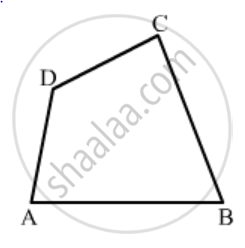
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of adjacent angles.
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
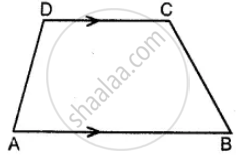
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
The diagonals of a rhombus are 6 .cm and 8 cm. State the angle at which these diagonals intersect.
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =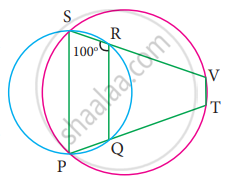
In quadrilateral ROPE, the pairs of adjacent angles are ______.
A quadrilateral can be drawn when all the four angles and one side is given.
Both the pairs of opposite angles of a quadrilateral are equal and supplementary. Find the measure of each angle.
Number of angles less than 180° in figure is ______ and their names are ______.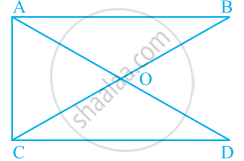
In given figure, What is BD – DE?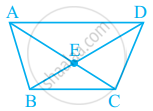
Using the information given, name the right angles in part of figure:
RS ⊥ RW
