Advertisements
Advertisements
Question
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
Solution
A quadrilateral is a polygon with four sides
∴ Sum of interior angles
= (n - 2) x 180°
= (4 - 2) x 180°
= 2 x 180°
= 360°
Ratio of the angles
= 1: 4: 5: 2
∴ The interior angles are x°, 4x°, 5x° and 2x°.
∴ x + 4x° + 5x° + 2x° = 360°
⇒ 12x° = 360°
⇒ x° = 30°
∴ The interior angles of the quadrilateral are 30°, 120°, 150° and 60°.
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
The sum of the angles of a quiadrilateral is .... right angles.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite angles are there?
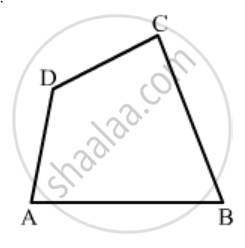
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
Which of the following quadrilateral is not a rhombus?
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?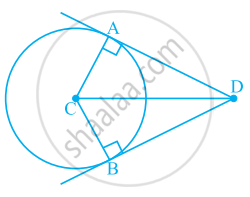
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
