Advertisements
Advertisements
Question
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
Solution
A pentagon has 5 sides
∴ Sum of interior angles
= (n - 2) x 180°
= (5 - 2) x 180°
= 3 x 180°
= 540°
Given, the angles are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°
∴ x °+ (x - 10)° + (x + 20)° + (2x - 44)° + (2x - 70)° = 540°
⇒ 7x° - 104° = 540°
⇒ x = `((540° + 104°))/(7)` = 92°
∴ The interior angles of the pentagon are 92°, 82°, 112°, 140° and 114°.
APPEARS IN
RELATED QUESTIONS
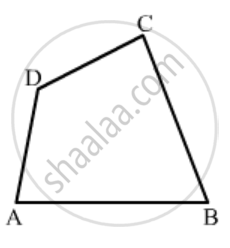
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of adjacent sides.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent angles are there?
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
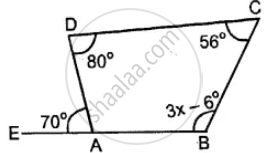
Use the information given in the following figure to find the value of x.
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
In quadrilateral WXYZ, the pairs of opposite angles are ______.
The number of common points in the two angles marked in figure is ______.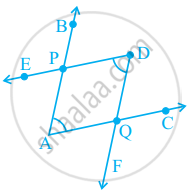
Using the information given, name the right angles in part of figure:
AC ⊥ BD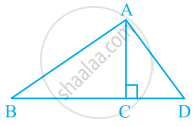
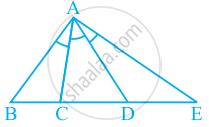
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?