Advertisements
Advertisements
Question
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
Options
10 cm
12 cm
14 cm
16 cm
Solution
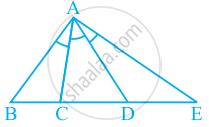
The given trapezium ABCD can be drawn as follows:

Here, AB || CD.
M and N are the mid-points of AD and BC respectively.
We have AB = 12cm ,MN = 14cm.
We need to find CD.
Join MN to intersect AC at G.
We have AB || CD and a line MN formed by joining the mid-points of sides AD and BC.
Thus, we can say that MN || AB || CD
In ΔADC M is the mid-point of AD and MG || CD
Therefore, G is the mid point of AC
By using the converse of mid-point theorem, we get:
`MG = 1/2 CD`…… (i)
In ΔABC, N is the mid point of BC and GN || AB
By using the converse of mid-point theorem, we get:
`GN = 1/2 AB` …… (ii)
Adding (i) and (ii),we get:
`GN + MG = 1/2AB +1/2 CD`
`MN = 1/2 (AB + CD)`…… (iii)
On substituting AB = 12cm and MN = 14cm in (iii),we get:
`14cm = 1/2(12cm + CD)`
28cm = 12cm + CD
CD = (28 - 12)cm
CD = 16cm
Hence the correct choice is (d).
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A triangle
In a quadrilateral, define of the following Angles .
In a quadrilateral, define of the following Diagonals .
In a quadrilateral, define of the following Exterior .
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
PQRSTU is a regular hexagon. Determine each angle of ΔPQT.
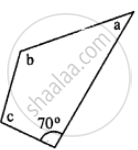
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
Using the information given, name the right angles in part of figure:
AE ⊥ CE
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?