Advertisements
Advertisements
Question
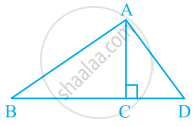
PQRSTU is a regular hexagon. Determine each angle of ΔPQT.
Solution

\[\text{ A regular hexagon is made up of 6 equilateral triangles } . \]
\[So, ∠PQT = 60° \text{ and } ∠QTP = 30° \]
\[\text{ Since the sum of the angles of ∆ PQT is } 180° , \text{ we have } : \]
\[ ∠P + ∠Q + ∠T = 180\]
\[ \Rightarrow ∠P + 60° + 30°= 180° \]
\[ \Rightarrow ∠P = 180° - 90° \]
\[ \Rightarrow ∠QPT = 90° \]
\[ \therefore \text{ The angles of the triangle are 90° , 60° and } 30° .\]
APPEARS IN
RELATED QUESTIONS
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent sides are there?
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
If the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C + ∠D = k ∠AOB, then find the value of k.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
Two adjacent angles of a parallelogram are 70° and 110° respectively. Find the other two angles of it.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is ______.
The number of common points in the two angles marked in figure is ______.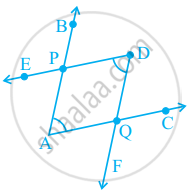
Using the information given, name the right angles in part of figure:
AC ⊥ BD