Advertisements
Advertisements
Question
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
Solution
\[\text{ Let n be the number of sides of a polygon } . \]
\[\text { Let x and 5x be the exterior and interior angles } . \]
\[\text{ Since the sum of an interior and the corresponding exterior angle is } 180° , \text{ we have } : \]
\[x + 5x = 180° \]
\[ \Rightarrow 6x = 180° \]
\[ \Rightarrow x = 30° \]
\[\text{ The polygon has n sides } . \]
\[\text{ So, sum of all the exterior angles } = \left( 30n \right)° \]
\[\text{ We know that the sum of all the exterior angles of a polygon is } 360° . \]
\[i . e . , 30n = 360\]
\[ \therefore n = 12\]
APPEARS IN
RELATED QUESTIONS
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of adjacent angles.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
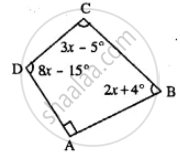
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
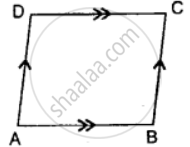
Write two conditions that will make the adjoining figure a square.
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is ______.
Which of the following is not true for a parallelogram?
In quadrilateral ROPE, the pairs of adjacent angles are ______.
In figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is ______.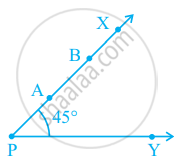
The common part between the two angles BAC and DAB in figure is ______.
