Advertisements
Advertisements
प्रश्न
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
उत्तर
\[\text{ Let n be the number of sides of a polygon } . \]
\[\text { Let x and 5x be the exterior and interior angles } . \]
\[\text{ Since the sum of an interior and the corresponding exterior angle is } 180° , \text{ we have } : \]
\[x + 5x = 180° \]
\[ \Rightarrow 6x = 180° \]
\[ \Rightarrow x = 30° \]
\[\text{ The polygon has n sides } . \]
\[\text{ So, sum of all the exterior angles } = \left( 30n \right)° \]
\[\text{ We know that the sum of all the exterior angles of a polygon is } 360° . \]
\[i . e . , 30n = 360\]
\[ \therefore n = 12\]
APPEARS IN
संबंधित प्रश्न
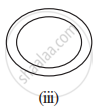
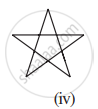
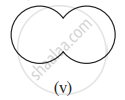
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
How many diagonals does following have?
A convex quadrilateral
In a quadrilateral, define of the following Opposite sides .
If ABCD is a rectangle with ∠BAC = 32°, find the measure of ∠DBC.
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
