Advertisements
Advertisements
प्रश्न
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sided of the polygon.
उत्तर
\[\left\{ \left( 2n - 4 \right) \times 90° \right\} = 3 \times \left( \frac{360° }{n} \times n \right)\]
\[ \Rightarrow \left( n - 2 \right) \times 180 = 3 \times 360\]
\[ \Rightarrow n - 2 = 6\]
\[ \therefore n = 8\]
APPEARS IN
संबंधित प्रश्न
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite angles are there?
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
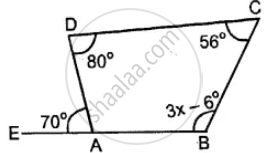
Use the information given in the following figure to find the value of x.
Two adjacent angles of a parallelogram are 70° and 110° respectively. Find the other two angles of it.
In parallelogram ABCD, its diagonals intersect at point O. If OA = 6 cm and OB = 7.5 cm, find the length of AC and BD.

In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
Using the information given, name the right angles in part of figure:
BA ⊥BD