Advertisements
Advertisements
प्रश्न
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sided of the polygon.
उत्तर
\[\left\{ \left( 2n - 4 \right) \times 90° \right\} = 3 \times \left( \frac{360° }{n} \times n \right)\]
\[ \Rightarrow \left( n - 2 \right) \times 180 = 3 \times 360\]
\[ \Rightarrow n - 2 = 6\]
\[ \therefore n = 8\]
APPEARS IN
संबंधित प्रश्न
Complete of the following, so as to make a true statement:
The number of pairs of opposite angles of a quadrilateral is .......
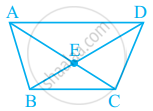
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of opposite sides are there?
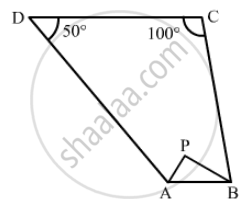
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
If ABCD is a rectangle with ∠BAC = 32°, find the measure of ∠DBC.
Write two conditions that will make the adjoining figure a square.
Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is ______.
In quadrilateral WXYZ, the pairs of opposite angles are ______.
In the given figure.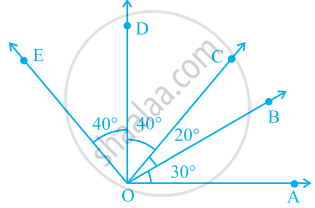
∠AOD is a/an ____ angle
Number of angles less than 180° in figure is ______ and their names are ______.
In given figure, What is BD – DE?