Advertisements
Advertisements
प्रश्न
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
उत्तर
\[\text{ For a convex hexagon, interior angle } = \left( \frac{2n - 4}{n} \times 90° \right)\]
\[\text{ For a hexagon,} n = 6\]
\[ \therefore \text{ Interior angle } = \left( \frac{12 - 4}{6} \times 90° \right)\]
\[ = \left( \frac{8}{6} \times 90° \right)\]
\[ = 120°\]
\[\text{ So, the sum of all the interior angles } = 120° + 120° + 120° + 120° + 120° + 120° = 720° \]
\[ \therefore \text{ Exterior angle } = \left( \frac{360}{n} \right)^° = \left( \frac{360}{6} \right)^° = {60}^° \]
\[\text{ So, sum of all the exterior angles } = {60}^° + {60}^° + {60}^° + {60}^° + {60}^° + {60}^° = {360}^° \]
\[\text{ Now, sum of all interior angles } = 720° \]
\[ = 2\left( 360° \right)\]
\[ = \text{ twice the exterior angles } \]
\[\text{ Hence proved } .\]
APPEARS IN
संबंधित प्रश्न
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
In a quadrilateral, define of the following Adjacent sides .
In a quadrilateral, define of the following Opposite angles .
Complete of the following, so as to make a true statement:
A quadrilateral has ....... sides.
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
A pair of opposite sides of a trapezium are ______.
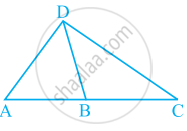
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?