Advertisements
Advertisements
प्रश्न
In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
उत्तर
\[\text{ For a convex hexagon, interior angle } = \left( \frac{2n - 4}{n} \times 90° \right)\]
\[\text{ For a hexagon,} n = 6\]
\[ \therefore \text{ Interior angle } = \left( \frac{12 - 4}{6} \times 90° \right)\]
\[ = \left( \frac{8}{6} \times 90° \right)\]
\[ = 120°\]
\[\text{ So, the sum of all the interior angles } = 120° + 120° + 120° + 120° + 120° + 120° = 720° \]
\[ \therefore \text{ Exterior angle } = \left( \frac{360}{n} \right)^° = \left( \frac{360}{6} \right)^° = {60}^° \]
\[\text{ So, sum of all the exterior angles } = {60}^° + {60}^° + {60}^° + {60}^° + {60}^° + {60}^° = {360}^° \]
\[\text{ Now, sum of all interior angles } = 720° \]
\[ = 2\left( 360° \right)\]
\[ = \text{ twice the exterior angles } \]
\[\text{ Hence proved } .\]
APPEARS IN
संबंधित प्रश्न
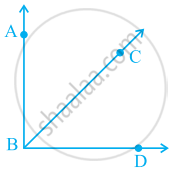
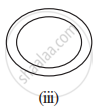
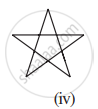
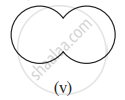
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
What is the sum of the measures of the angels of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Complete of the following, so as to make a true statement:
A quadrilateral has ....... sides.
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Complete the following statement by means of one of those given in brackets against each:
A line drawn from the mid-point of one side of a triangle .............. another side intersects the third side at its mid-point.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
From the following figure find;
- x
- ∠ABC
- ∠ACD
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a+2)° and ∠B = 2(2a+7)°.
Calculate ∠A.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles
Using the information given, name the right angles in part of figure:
BA ⊥BD