Advertisements
Advertisements
Question
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sided of the polygon.
Solution
\[\left\{ \left( 2n - 4 \right) \times 90° \right\} = 3 \times \left( \frac{360° }{n} \times n \right)\]
\[ \Rightarrow \left( n - 2 \right) \times 180 = 3 \times 360\]
\[ \Rightarrow n - 2 = 6\]
\[ \therefore n = 8\]
APPEARS IN
RELATED QUESTIONS
The perimeter of a parallelogram is 22 cm . If the longer side measures 6.5 cm what is the measure of the shorter side?
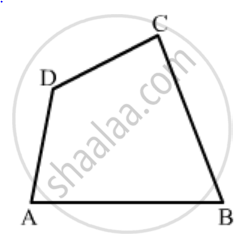
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent angles are there?
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
A quadrilateral has three acute angles each measures 80°. What is the measure of the fourth angle?
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
Mark the correct alternative in each of the following:
The opposite sides of a quadrilateral have
Find the angles of a pentagon which are in the ratio 4: 4: 6: 7: 6.
In figure, ∠XYZ cannot be written as ______.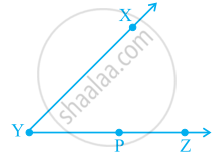
The number of straight angles in figure is ______.