Advertisements
Advertisements
Question
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
Solution
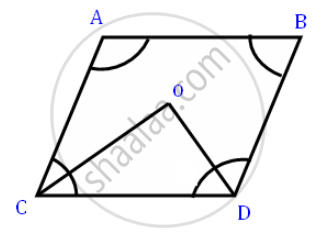
\[ ∠COD = 180° - \left(∠OCD + ∠ODC \right)\]
\[ = 180°- \frac{1}{2}\left(∠C + ∠D \right)\]
\[ = 180°- \frac{1}{2}\left[ 360° - \left(∠A + ∠B \right) \right]\]
\[ = 180°- 180°+ \frac{1}{2}\left( ∠A + ∠B \right)\]
\[ = \frac{1}{2}\left( ∠A +∠B \right)\]
\[ = RHS\]
\[\text{ Hence proved } .\]
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Interior .
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
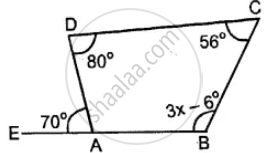
Use the information given in the following figure to find the value of x.
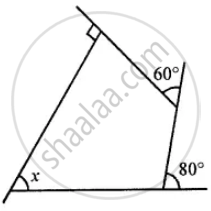
Use the following figure to find the value of x
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.
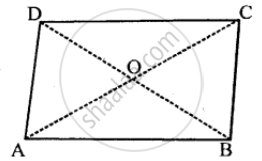
If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
In the given figure.
∠AOE is a/an ______ angle
