Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
उत्तर
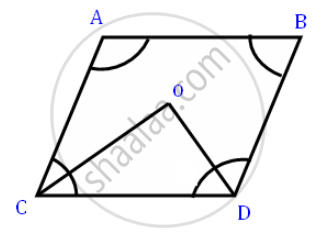
\[ ∠COD = 180° - \left(∠OCD + ∠ODC \right)\]
\[ = 180°- \frac{1}{2}\left(∠C + ∠D \right)\]
\[ = 180°- \frac{1}{2}\left[ 360° - \left(∠A + ∠B \right) \right]\]
\[ = 180°- 180°+ \frac{1}{2}\left( ∠A + ∠B \right)\]
\[ = \frac{1}{2}\left( ∠A +∠B \right)\]
\[ = RHS\]
\[\text{ Hence proved } .\]
APPEARS IN
संबंधित प्रश्न
In a quadrilateral, define of the following Opposite angles .
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
The diagonals of a rhombus are 6 .cm and 8 cm. State the angle at which these diagonals intersect.
Observe the figure below and find out their name.
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
In figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is ______.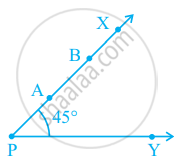
Using the information given, name the right angles in part of figure:
BA ⊥BD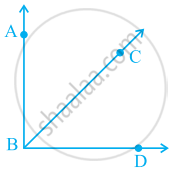
Using the information given, name the right angles in part of figure:
RT ⊥ ST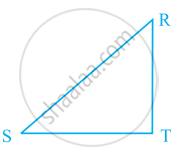
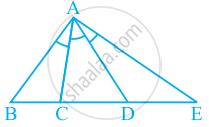
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?