Advertisements
Advertisements
प्रश्न
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?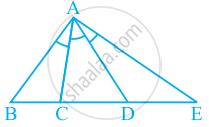
उत्तर
For an angle to be trisected, we need two trisectors. So, for ∠BAE, we have two trisectors, i.e. AC and AD. AC and AD divides the ∠BAE in three equal angles.
APPEARS IN
संबंधित प्रश्न
In a quadrilateral, define of the following Interior .
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
One angle of a hexagon is 140° and the remaining angles are in the ratio 4 : 3 : 4 : 5 : 4. Calculate the measures of the smallest and the largest angles.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
The diagonals of the quadrilateral DEFG are ______ and ______.
The number of common points in the two angles marked in figure is ______.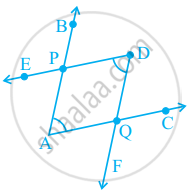
In given figure, What is AE + EC?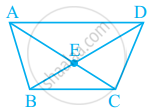
Using the information given, name the right angles in part of figure:
AC ⊥ BD