Advertisements
Advertisements
प्रश्न
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?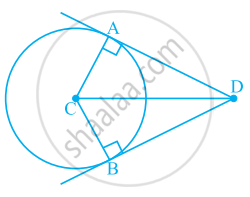
उत्तर
If DC is the bisector of ∠ADB, then ∠ADC = ∠BDC.
Also, CA ⊥ DA and CB ⊥ DB, then ∠CAD = 90° and ∠CBD = 90°
APPEARS IN
संबंधित प्रश्न
In a quadrilateral, define of the following Adjacent angles .
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
Complete of the following, so as to make a true statement:
The measure of each angle of a convex quadrilateral is ..... 180°.
Three angles of a quadrilateral are equal. Fourth angle is of measure 150°. What is the measure of equal angles.
Complete the following statement by means of one of those given in brackets against each:
f consecutive sides of a parallelogram are equal, then it is necessarily a ..................
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.
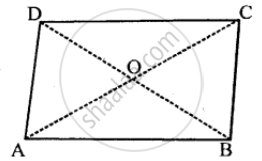
If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
In the given figure.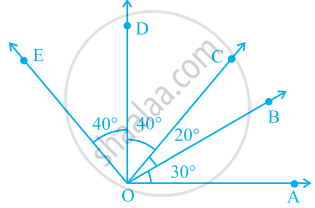
∠AOD is a/an ____ angle
