Advertisements
Advertisements
प्रश्न
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
उत्तर
A quadrilateral is a polygon with four sides
∴ Sum of interior angles
= (n - 2) x 180°
= (4 - 2) x 180°
= 2 x 180°
= 360°
Ratio of the angles
= 1: 4: 5: 2
∴ The interior angles are x°, 4x°, 5x° and 2x°.
∴ x + 4x° + 5x° + 2x° = 360°
⇒ 12x° = 360°
⇒ x° = 30°
∴ The interior angles of the quadrilateral are 30°, 120°, 150° and 60°.
APPEARS IN
संबंधित प्रश्न
In a quadrilateral, define of the following Opposite sides .
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
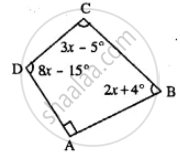
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
ABCDE is a pentagon in which AB is parallel to DC and ∠A : ∠E : ∠D = 1 : 2 : 3. Find angle A.
What is the maximum number of obtuse angles that a quadrilateral can have?
The diagonals of the quadrilateral DEFG are ______ and ______.
The number of right angles in a straight angle is ______ and that in a complete angle is ______.
