Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
उत्तर
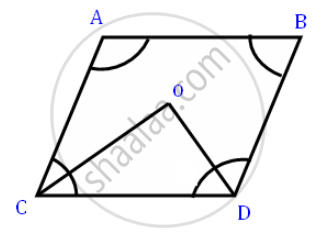
\[ ∠COD = 180° - \left(∠OCD + ∠ODC \right)\]
\[ = 180°- \frac{1}{2}\left(∠C + ∠D \right)\]
\[ = 180°- \frac{1}{2}\left[ 360° - \left(∠A + ∠B \right) \right]\]
\[ = 180°- 180°+ \frac{1}{2}\left( ∠A + ∠B \right)\]
\[ = \frac{1}{2}\left( ∠A +∠B \right)\]
\[ = RHS\]
\[\text{ Hence proved } .\]
APPEARS IN
संबंधित प्रश्न
Define the following term Quadrilateral .
Complete of the following, so as to make a true statement:
A quadrilateral has ..... vertices, no three of which are .....
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
Complete the following statement by means of one of those given in brackets against each:
If opposite angles of a quadrilateral are equal, then it is necessarily a ....................
The angles A, B, C and D of a trapezium ABCD are in the ratio 3: 4: 5: 6. Le. ∠A : ∠B : ∠C : ∠D = 3:4: 5 : 6. Find all the angles of the trapezium. Also, name the two sides of this trapezium which are parallel to each other. Give reason for your answer.
Write two conditions that will make the adjoining figure a square.
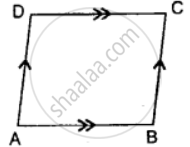
If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3 : 7 : 6 : 4, then ABCD is a ______.
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?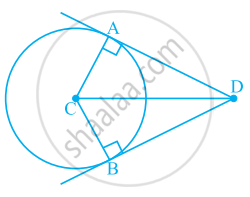
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent sides.
