Advertisements
Advertisements
Question
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
Solution
\[\text{ Let x be the measure of each angle } . \]
\[\text{ Then the ratio becomes x : 2x : 4x : 5x .} \]
\[ \text{ Since, the sum of all angles in a quadrilateral is } 360° , \text{ we have } : \]
\[x + 2x + 4x + 5x = 360° \]
\[ \Rightarrow 12x = 360° \]
\[ \Rightarrow x = \frac{360° }{12}\]
\[ \Rightarrow x = 30° \]
\[\text{ Thus, the angles are } : \]
\[x = 30 ° \]
\[2x = 60° \]
\[4x = 120° \]
\[5x = 150° \]
APPEARS IN
RELATED QUESTIONS
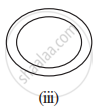
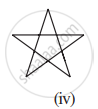
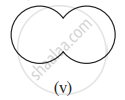
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
A quadrilateral has three acute angles each measures 80°. What is the measure of the fourth angle?
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
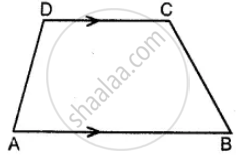
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
In quadrilateral ROPE, the pairs of adjacent angles are ______.
Measures of the two angles between hour and minute hands of a clock at 9 O’ clock are ______.
Using the information given, name the right angles in part of figure:
RT ⊥ ST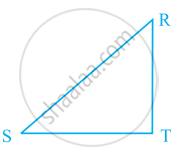
What conclusion can be drawn from part of given figure, if BD bisects ∠ABC?
