Advertisements
Advertisements
Question
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
Solution
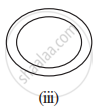
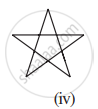
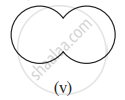
- Simple curve: It is a curve that does not intersect itself. (i), (ii), (v), (vi) and (vii) are simple curve.
- Simple closed curve: A closed curve if it does not pass through one point more than once (i), (ii), (v), (vi) and (vii) are simple closed curve.
- Polygon: A simple closed curve made up of only line segments is called a polygon. (i) and (ii) are polygons.
- Convex polygon: A polygon that has all its interior angles less than 180°. (ii) is a convex polygon.
- Concave polygon: A polygon that has at least one interior angle greater than 180°. (i) is a concave polygon.
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
A quadrilateral has ..... vertices, no three of which are .....
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
Which of the following quadrilateral is not a rhombus?
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.
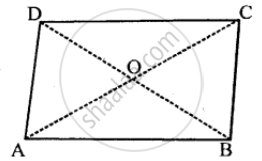
If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
The angles of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
What conclusion can be drawn from part of given figure, if BD bisects ∠ABC?
