Advertisements
Advertisements
Question
The angles of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
Solution
A hexagon has 6 sides
∴ Sum of interior angles
= (n - 2) x 180°
= (6 - 2) x 180°
= 4 x 180°
= 720°
Given the angle of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°
∴ (2x + 5)°, + (3x - 5)°, + (x + 40)°, + (2x + 20)°, + (2x + 25)° +(2x + 35)° = 720
⇒ 12x + 120° = 720°
⇒ x = 50°.
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A convex quadrilateral
Complete of the following, so as to make a true statement:
A diagonal of a quadrilateral is a line segment that joins two ...... vertices of the quadrilateral.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent sides are there?
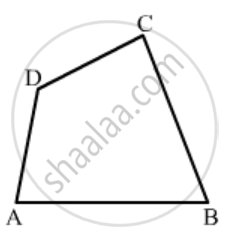
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
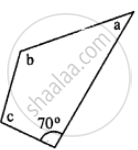
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
Find the angles of a pentagon which are in the ratio 4: 4: 6: 7: 6.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
Using the information given, name the right angles in part of figure:
RS ⊥ RW
Using the information given, name the right angles in part of figure:
OP ⊥ AB