Advertisements
Advertisements
Question
One angle of a hexagon is 140° and the remaining angles are in the ratio 4 : 3 : 4 : 5 : 4. Calculate the measures of the smallest and the largest angles.
Solution
A hexagon has 6 sides
∴ Sum of interior angles
= (n - 2) x 180°
= (6- 2) x 180°
= 4 x 180° = 720°
One angle is given to be 140°
Ratio of the remaining five angles
= 4 : 3 : 4 : 5: 4
∴ The interior angles are 4x°, 3x°, 4x°, 5x° and 4x°
∴ 140° + 4x° + 3x° + 4x° + 5° + 4x° = 720°
⇒ 20x° + 140° = 720°
⇒ x° = `(580°)/(20)` = 29°
The smallest angle is 3x° = 3.29° = 87°
The largest angle is 5x° = 5.29° = 145°.
APPEARS IN
RELATED QUESTIONS
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
Which of the following quadrilateral is not a rhombus?
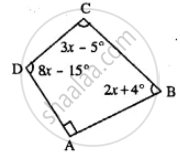
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120. find angles B and D.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
One diagonal of a rectangle is 18 cm. What is the length of its other diagonal?
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is
The number of common points in the two angles marked in figure is ______.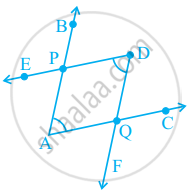
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite angles.
