Advertisements
Advertisements
प्रश्न
The angles of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
उत्तर
A hexagon has 6 sides
∴ Sum of interior angles
= (n - 2) x 180°
= (6 - 2) x 180°
= 4 x 180°
= 720°
Given the angle of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°
∴ (2x + 5)°, + (3x - 5)°, + (x + 40)°, + (2x + 20)°, + (2x + 25)° +(2x + 35)° = 720
⇒ 12x + 120° = 720°
⇒ x = 50°.
APPEARS IN
संबंधित प्रश्न
Calculate the measure of each angle of a nonagon.
Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is ______.
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is ______.
What is the maximum number of obtuse angles that a quadrilateral can have?
If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?
In given figure, What is BD – BE?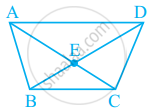
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?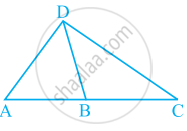
Can we have two obtuse angles whose sum is a complete angle? Why or why not?
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent sides.
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
