Advertisements
Advertisements
Question
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
Solution
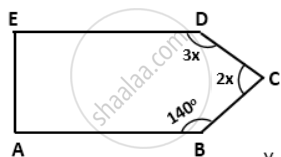
Since AB || ED, we have
∠A + ∠E = 180°
Now,
∠A + ∠B + ∠C + ∠D + ∠E = (5 - 2) x 180°
⇒ (∠A + ∠E) + 140° + 2x + 3x = 3 x 180°
⇒ 180° + 140° + 5x = 540°
⇒ 320° + 5x = 540°
⇒ 5x = 220°
⇒ x = 44°
Hence,
∠C = 2x = 2 x 44° = 88°
∠D = 3x = 3 x 44° = 132°.
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Diagonals .
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
PQRSTU is a regular hexagon. Determine each angle of ΔPQT.
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is ______.
ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.
A quadrilateral can have all four angles as obtuse.
In figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is ______.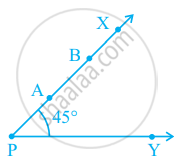
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?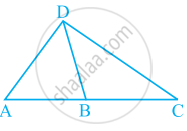
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite sides.
