Advertisements
Advertisements
Question
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
Options
40º
45º
50º
60º
Solution
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is 50º.
Explanation:
Given, ABCD is a rhombus such that ∠ACB = 40º ⇒ ∠OCB = 40º
Since, AD || BC
∠DAC = ∠BCA = 40º ...[Alternate interior angles]
Also, ∠AOD = 90º ...[Diagonals of a rhombus are perpendicular to each other]
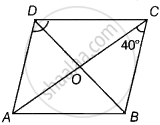
We know that, sum of all angles of a triangle ADO is 180º
∴ ∠ADO + ∠DOA + ∠OAD = 180º
∴ ∠ADO = 180º – (40º + 90º)
= 180º – 130º
= 50º
⇒ ∠ADB = 50º
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Interior .
Complete of the following, so as to make a true statement:
A quadrilateral has ....... sides.
Complete of the following, so as to make a true statement:
The measure of each angle of a convex quadrilateral is ..... 180°.
Complete of the following, so as to make a true statement:
A quadrilateral is convex if, for each side, the remaining ______ lie on the same side of the line containing the side.
The measure of angles of a hexagon are x°, (x − 5)°, (x − 5)°, (2x − 5)°, (2x − 5)°, (2x + 20)°. Find the value of x.
If the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C + ∠D = k ∠AOB, then find the value of k.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
If three angles of a quadrilateral are 90° each, show that the given quadrilateral is a rectangle.
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
