Advertisements
Advertisements
प्रश्न
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
विकल्प
40º
45º
50º
60º
उत्तर
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is 50º.
Explanation:
Given, ABCD is a rhombus such that ∠ACB = 40º ⇒ ∠OCB = 40º
Since, AD || BC
∠DAC = ∠BCA = 40º ...[Alternate interior angles]
Also, ∠AOD = 90º ...[Diagonals of a rhombus are perpendicular to each other]
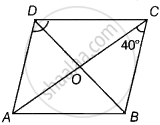
We know that, sum of all angles of a triangle ADO is 180º
∴ ∠ADO + ∠DOA + ∠OAD = 180º
∴ ∠ADO = 180º – (40º + 90º)
= 180º – 130º
= 50º
⇒ ∠ADB = 50º
APPEARS IN
संबंधित प्रश्न
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
In a quadrilateral, define of the following Interior .
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Find the angles of a quadrilateral whose angles are in the ratio 1: 4: 5: 2.
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
In given figure, What is BD – DE?