Advertisements
Advertisements
प्रश्न
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
विकल्प
rectangle
rhombus
parallelogram
quadrilateral whose opposite angles are supplementary
उत्तर
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a quadrilateral whose opposite angles are supplementary
Explanation:
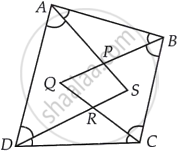
Sum of all angles of a quadrilateral is 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
On dividing both sides by 2,
⇒ `1/2` (∠A + ∠B + ∠C + ∠D) = `1/2` × 360° = 180°
∵ AP, PB, RC and RD are bisectors of ∠A, ∠B, ∠C and ∠D
⇒ ∠PAB + ∠ABB + ∠RCD + ∠RDC = 180° ...(1)
Sum of all angles of a triangle is 180°
∴ ∠PAB + ∠APB + ∠ABP = 180°
⇒ ∠PAB + ∠ABP = 180° – ∠APB ...(2)
Similarly,
∴ ∠RDC + ∠RCD + ∠CRD = 180°
⇒ ∠RDC + ∠RCD = 180° – ∠CRD ...(3)
Putting (2) and (3) in (1),
180° – ∠APB + 180° – ∠CRD = 180°
⇒ 360° – ∠APB – ∠CRD = 180°
⇒ ∠APB + ∠CRD = 360° – 180°
⇒ ∠APB + ∠CRD = 180° ...(4)
Now,
∠SPQ = ∠APB ...[Vertically opposite angles]
∠SRQ = ∠DRC ...[Vertically opposite angles]
Putting in (4),
⇒ ∠SPQ + ∠SRQ = 180°
APPEARS IN
संबंधित प्रश्न
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of adjacent sides.
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
PQRSTU is a regular hexagon. Determine each angle of ΔPQT.
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
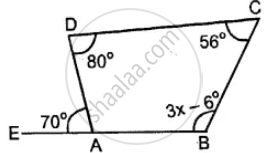
Use the information given in the following figure to find the value of x.
Calculate the measure of each angle of a nonagon.
In given figure, name any four angles that appear to be acute angles.
Using the information given, name the right angles in part of figure:
RS ⊥ RW
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
