Advertisements
Advertisements
प्रश्न
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form ______.
विकल्प
a square
a rhombus
a rectangle
any other parallelogram
उत्तर
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form a rectangle.
Explanation:
Given, APB and CQD are two parallel lines.
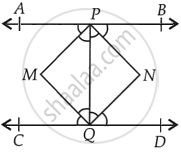
Let the bisectors of angles APQ and CQP meet at a point M and bisectors of angles BPQ and PQD meet at a point N.
Join PM, MQ, QN and NP.
Since, APB || CQD
Then, ∠APQ = ∠PQD ...[Alternate interior angles]
⇒ ∠MPQ = 2∠NQP ...[Since, PM and NQ are the angle bisectors of ∠APQ and ∠DQP respectively]
⇒ ∠MPQ = ∠NQP ...[Dividing both sides by 2] [Since, alternative interior angles are equal]
∴ PM || QN
Similarly, ∠BPQ = ∠CQP ...[Alternate interior angles]
∴ PN || QM
So, quadrilateral PMQN is a parallelogram.
∵ ∠CQD = 180° ...[Since, CQD is a line]
⇒ ∠CQP + ∠DQP = 180°
⇒ 2∠MQP + 2∠NQP = 180° ...[Since, MQ and NQ are the bisectors of the angles CQP and DQP]
⇒ 2(∠MQP + ∠NQP) = 180°
⇒ ∠MQN = 90°
Hence, PMQN is a rectangle.
APPEARS IN
संबंधित प्रश्न
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
In a quadrilateral, define of the following Exterior .
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
Complete the following statement by means of one of those given in brackets against each:
f consecutive sides of a parallelogram are equal, then it is necessarily a ..................
Write two conditions that will make the adjoining figure a square.
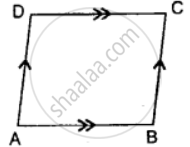
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
Calculate the measure of each angle of a nonagon.
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
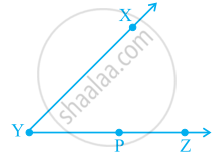
In figure, ∠XYZ cannot be written as ______.