Advertisements
Advertisements
प्रश्न
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form ______.
पर्याय
a square
a rhombus
a rectangle
any other parallelogram
उत्तर
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form a rectangle.
Explanation:
Given, APB and CQD are two parallel lines.
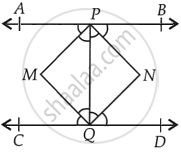
Let the bisectors of angles APQ and CQP meet at a point M and bisectors of angles BPQ and PQD meet at a point N.
Join PM, MQ, QN and NP.
Since, APB || CQD
Then, ∠APQ = ∠PQD ...[Alternate interior angles]
⇒ ∠MPQ = 2∠NQP ...[Since, PM and NQ are the angle bisectors of ∠APQ and ∠DQP respectively]
⇒ ∠MPQ = ∠NQP ...[Dividing both sides by 2] [Since, alternative interior angles are equal]
∴ PM || QN
Similarly, ∠BPQ = ∠CQP ...[Alternate interior angles]
∴ PN || QM
So, quadrilateral PMQN is a parallelogram.
∵ ∠CQD = 180° ...[Since, CQD is a line]
⇒ ∠CQP + ∠DQP = 180°
⇒ 2∠MQP + 2∠NQP = 180° ...[Since, MQ and NQ are the bisectors of the angles CQP and DQP]
⇒ 2(∠MQP + ∠NQP) = 180°
⇒ ∠MQN = 90°
Hence, PMQN is a rectangle.
APPEARS IN
संबंधित प्रश्न
The perimeter of a parallelogram is 22 cm . If the longer side measures 6.5 cm what is the measure of the shorter side?
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
In the given figure, ABCD is a trapezium. Find the values of x and y.

In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
The angles of a hexagon are (2x + 5)°, (3x - 5)°, (x + 40)°, (2x + 20)°, (2x + 25)° and (2x + 35)°. Find the value of x.
One angle of a pentagon is 160° and the rest are all equal angles. Find the measure of the equal angles.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =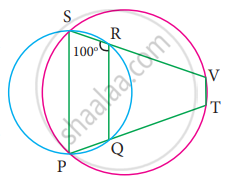
The diagonals of the quadrilateral DEFG are ______ and ______.
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
