Advertisements
Advertisements
प्रश्न
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
पर्याय
a rhombus
a rectangle
a square
any parallelogram
उत्तर
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is a rectangle.
Explanation:
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

Join AC, RP and SQ
In ∆ABC,
P is midpoint of AB and Q is midpoint of BC
∴ By midpoint theorem,
PQ || AC and PQ = `1/2` AC ...(1)
Similarly,
In ∆DAC,
S is midpoint of AD and R is midpoint of CD
∴ By midpoint theorem,
SR || AC and SR = `1/2` AC ...(2)
From (1) and (2),
PQ || SR and PQ = SR
⇒ PQRS is a parallelogram
ABQS is a parallelogram
⇒ AB = SQ
PBCR is a parallelogram
⇒ BC = PR
⇒ AB = PR ...[∵ BC = AB, sides of rhombus]
⇒ SQ = PR
∴ Diagonals of the parallelogram are equal.
Hence, it is a rectangle.
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
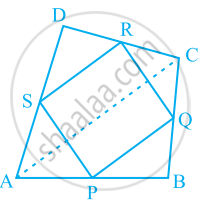
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
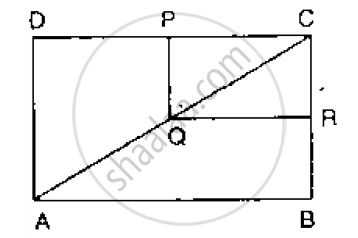
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
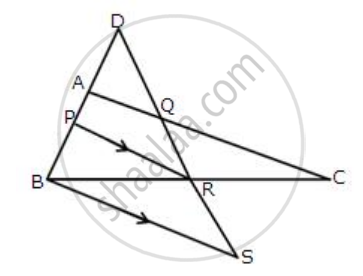
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.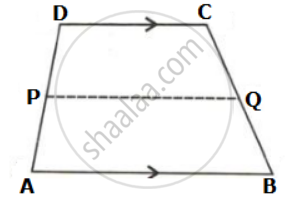
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
