Question

D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.

पर्याय

• a square

• a rectangle

• a rhombus

• a parallelogram

Answer 1

D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is a parallelogram.

Explanation:

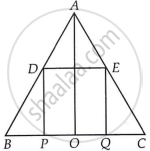
In ΔABC, D and E are the mid-points of sides AB and AC, respectively.

By mid-point theorem,

DE || BC  ...(i)

DE = `1/2` BC

Then, DE = `1/2` [BP + PO + OQ + QC]

DE = `1/2` [2PO + 2OQ]  ...[Since, P and Q are the mid-points of OB and OC respectively]

⇒ DE = PO + OQ

⇒ DE = PQ

Now, in ΔAOC, Q and E are the mid-points of OC and AC respectively.

∴ EQ || AO and EQ = `1/2` AO  [By mid-point theorem]  ...(iii)

Similarly, in ΔABO,

PD || AO and PD = `1/2` AO  [By mid-point theorem]  ...(iv)

From equations (iii) and (iv),

EQ || PD and EQ = PD

From equations (i) and (ii),

 DE || BC (or DE || PQ) and DE = PQ

Hence, DEQP is a parallelogram.