Advertisements
Advertisements
Question
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
Options
a square
a rectangle
a rhombus
a parallelogram
Solution
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is a parallelogram.
Explanation:
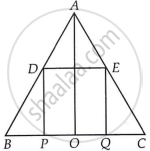
In ΔABC, D and E are the mid-points of sides AB and AC, respectively.
By mid-point theorem,
DE || BC ...(i)
DE = `1/2` BC
Then, DE = `1/2` [BP + PO + OQ + QC]
DE = `1/2` [2PO + 2OQ] ...[Since, P and Q are the mid-points of OB and OC respectively]
⇒ DE = PO + OQ
⇒ DE = PQ
Now, in ΔAOC, Q and E are the mid-points of OC and AC respectively.
∴ EQ || AO and EQ = `1/2` AO [By mid-point theorem] ...(iii)
Similarly, in ΔABO,
PD || AO and PD = `1/2` AO [By mid-point theorem] ...(iv)
From equations (iii) and (iv),
EQ || PD and EQ = PD
From equations (i) and (ii),
DE || BC (or DE || PQ) and DE = PQ
Hence, DEQP is a parallelogram.
APPEARS IN
RELATED QUESTIONS
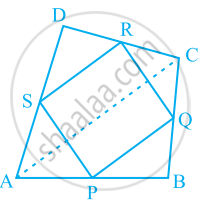
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

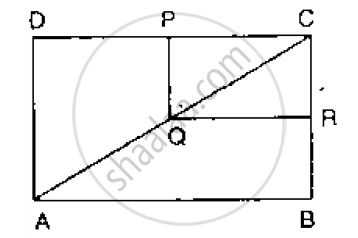
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm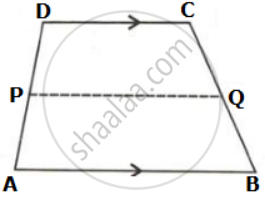
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
