Advertisements
Advertisements
Question
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
Solution
Given in the question, D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equivalent ∆ABC.
To proof that ∆DEF is an equilateral triangle.
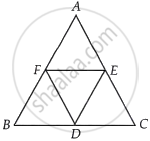
Proof: In ∆ABC, E and F are the mid-points of AC and AB respectively, then EF || BC.
So, EF = `1/2` BC ...(I)
DF || AC, DE || AB
DE = `1/2` AB and FD = `1/2` AC [By mid-point theorem] ...(II)
Now, ∆ABC is an equilateral triangle
AB = BC = CA
`1/2` AB = `1/2` BC = `1/2` CA ...[Dividing by 2 in the above equation]
So, DE = EF = FD ...[From equation (I) and (II)]
Since, all sides of ADEF are equal.
Hence, ∆DEF is an equilateral triangle
Hence proved.
APPEARS IN
RELATED QUESTIONS
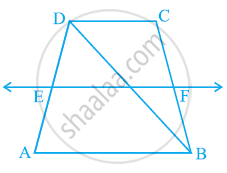
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
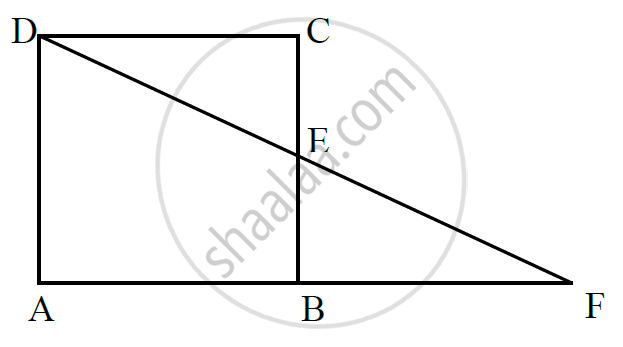
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
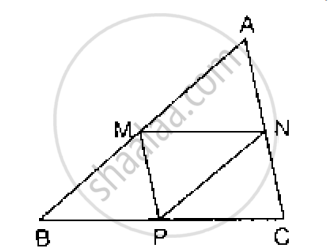
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm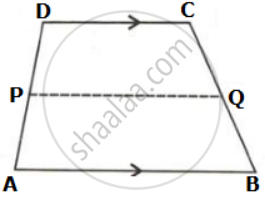
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: 2EF = BD.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
