Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Text
Draw a triangle and mark the mid-points E and F of two sides of the triangle. Join the points E and F in following fig. 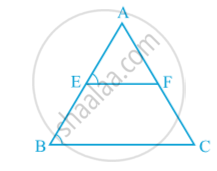
Measure EF and BC. Measure ∠ AEF and ∠ ABC. EF = `1/2` BC and ∠ AEF = ∠ ABC
so, EF || BC
Theorem
Theorem : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Observe following Fig. in which E and F are mid-points of AB and AC respectively and CD || BA.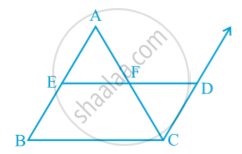
∆ AEF ≅ ∆ CDF (ASA Rule)
So, EF = DF and BE = AE = DC
Therefore, BCDE is a parallelogram.
This gives EF || BC.
In this case, also note that EF = `1/2` ED = `1/2` BC.
Theorem
Theorem : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
In following fig. 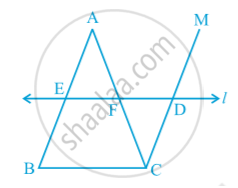
Observe that E is the mid-point of AB, line l is passsing through E and is parallel to BC and CM || BA.
Prove that AF = CF by using the congruence of ∆ AEF and ∆ CDF.