Advertisements
Advertisements
Question
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
Solution

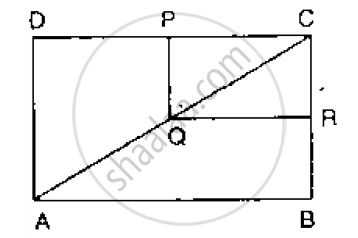
Given: Let ABCD be a rectangle where P, Q, R, S are the midpoint of AB, BC, CD, DA.
To Prove: PQRS is a rhombus
Construction: Draw two diagonal BD and AC as shown in figure. Where BD = AC
(Since diagonal of the rectangle are equal)
Proof:
From ΔABD and ΔBCD
PS = `1/2` BD = QR and PS || BD || QR
2PS = 2QR = BD and PS || QR ...(1)
Similarly, 2PQ = 2SR = AC and PQ || SR ...(2)
From (1) and (2) we get
PQ = QR = RS = PS
Therefore, PQRS is a rhombus.
Hence, proved.
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
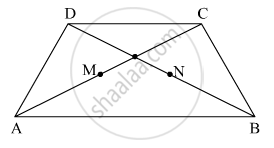
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.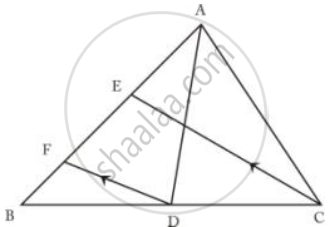
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: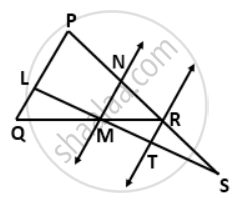
ST = `(1)/(3)"LS"`
