Advertisements
Advertisements
Question
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.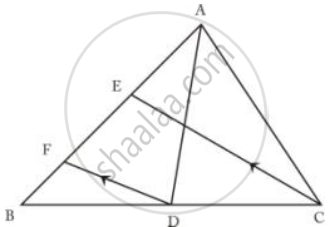
Solution
Given AD and CE are medians and DF || CE.
We know that from the midpoint theorem,
If two lines are parallel and the starting point of the segment is at the midpoint on one side, then the other point meets at the midpoint of the other side.
Consider triangle BEC. Given DF || CE and
D is the midpoint of BC.
So F must be the midpoint of BE.
So, FB = `1/2`BE but BE = `1/2`AB
Substitute value of BE in the first equation, we get
FB = `1/4`AB
Hence Proved.
APPEARS IN
RELATED QUESTIONS
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
