Advertisements
Advertisements
प्रश्न
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.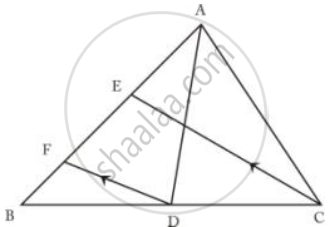
उत्तर
Given AD and CE are medians and DF || CE.
We know that from the midpoint theorem,
If two lines are parallel and the starting point of the segment is at the midpoint on one side, then the other point meets at the midpoint of the other side.
Consider triangle BEC. Given DF || CE and
D is the midpoint of BC.
So F must be the midpoint of BE.
So, FB = `1/2`BE but BE = `1/2`AB
Substitute value of BE in the first equation, we get
FB = `1/4`AB
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

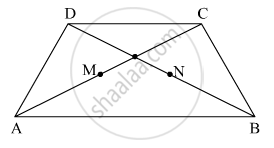
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
