Advertisements
Advertisements
प्रश्न
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
उत्तर
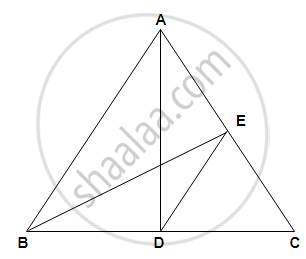
Since AD is the median of ΔABC, then BD = DC.
Given, DE || AB and DE are drawn from the midpoint of BC i.e. D, then
by the converse of mid-point theorem,
it bisects the third side which in this case is AC at E.
Therefore, E is the mid point of AC.
Hence, BE is the median of ΔABC.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
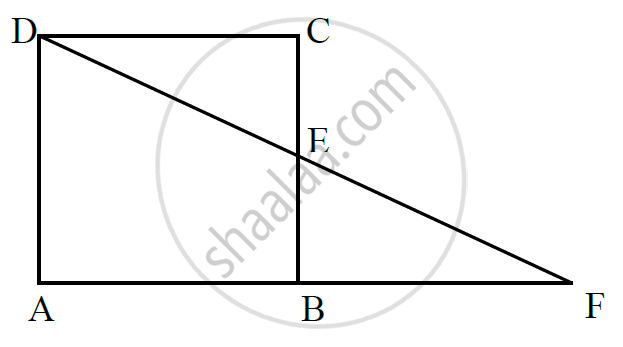
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
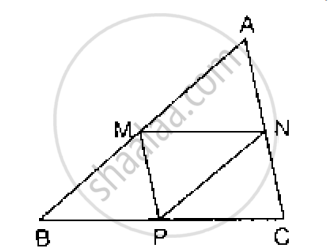
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: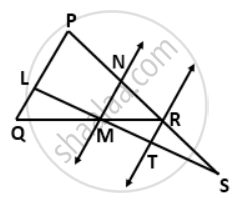
ST = `(1)/(3)"LS"`
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: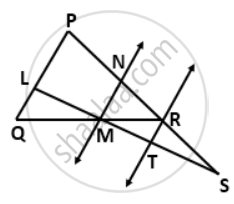
RT = `(1)/(3)"PQ"`
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
