Advertisements
Advertisements
प्रश्न
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
उत्तर
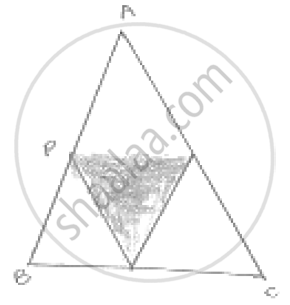
In ΔABC
R and P are the midpoint of AB and BC
∴RP || AC, RP = `1/2` AC [By midpoint theorem]
In a quadrilateral
[A pair of side is parallel and equal]
RP || AQ, RP = AQ
∴RPQA is a parallelogram
AR = `1/2` AB = `1/2 ` × 30 = 15cm
AR = QP = 15 [ ∵ Opposite sides are equal]
⇒ RP = `1/2` AC = `1/2` × 21 = 10 .5cm [ ∵ Opposite sides are equal]
Now,
Perimeter of ARPQ = AR + QP + RP + AQ
= 15 +15 +10.5 +10.5
= 51cm
APPEARS IN
संबंधित प्रश्न
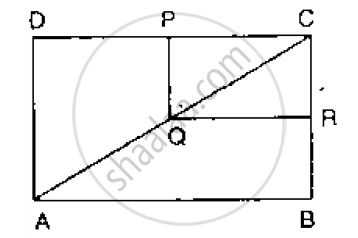
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm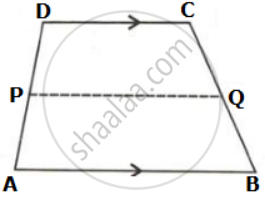
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
