Advertisements
Advertisements
प्रश्न
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
उत्तर
Given in the question, D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equivalent ∆ABC.
To proof that ∆DEF is an equilateral triangle.
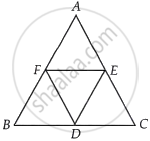
Proof: In ∆ABC, E and F are the mid-points of AC and AB respectively, then EF || BC.
So, EF = `1/2` BC ...(I)
DF || AC, DE || AB
DE = `1/2` AB and FD = `1/2` AC [By mid-point theorem] ...(II)
Now, ∆ABC is an equilateral triangle
AB = BC = CA
`1/2` AB = `1/2` BC = `1/2` CA ...[Dividing by 2 in the above equation]
So, DE = EF = FD ...[From equation (I) and (II)]
Since, all sides of ADEF are equal.
Hence, ∆DEF is an equilateral triangle
Hence proved.
APPEARS IN
संबंधित प्रश्न
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
