Advertisements
Advertisements
प्रश्न
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
उत्तर
To prove LM = LN
Draw LS perpendicular to line MN
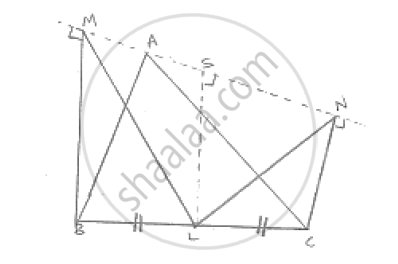
∴ The lines BM, LS and CN being the same perpendiculars, on line MN are parallel to each
other.
According to intercept theorem,
If there are three or more parallel lines and the intercepts made by them on a transversal or
equal. Then the corresponding intercepts on any other transversal are also equal.
In the drawn figure, MB and LS and NC are three parallel lines and the two transversal line
are MN and BC
We have, BL= LC (As L is the given midpoint of BC)
∴ using intercept theorem, we get
MS = SN ....(i )
Now in Δ MLS and LSN
MS = SN using ….(i)
`∠`LSM = `∠`LSN = 90°LS ^ MN and SL = LS common
∴ Δ DMLS ≅ Δ LSN (SAS congruency theorem)
∴ LM = LN (CPCT )
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
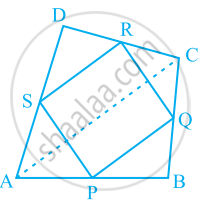
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.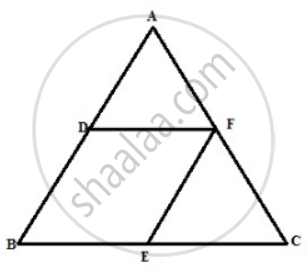
Remark: Figure is incorrect in Question
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
