Advertisements
Advertisements
प्रश्न
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
उत्तर
The figure is shown below
Since M and N are the mid-point of AB and AC, MN || BC
According to intercept theorem Since MN || BC and AM = BM,
Therefore AX = DX. Hence proved
APPEARS IN
संबंधित प्रश्न
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
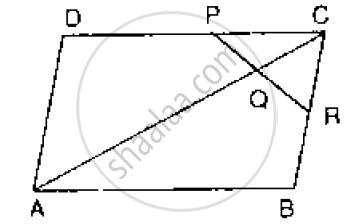
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
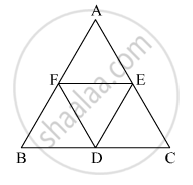
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.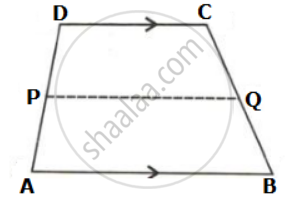
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: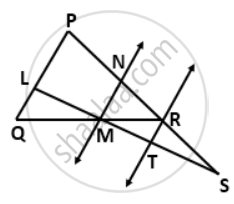
RT = `(1)/(3)"PQ"`
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
