Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
उत्तर
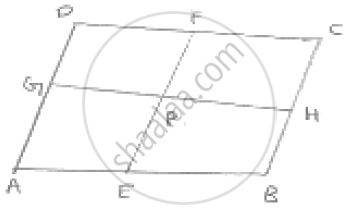
Since E and F are midpoints of AB and CD respectively
∴ AE = BE =`1/2` AB
And CF = DF =`1/2` CD
But, AB = CD
∴ `1/2` AB = `1/2` CD
⇒ BE = CF
Also, BE || CF [∵AB || CD]
∴ BEFC is a parallelogram
⇒ BC || EF and BF = PH ....(i )
Now, BC || EF
⇒ AD || EF [ ∵ BC || AD as ABCD is a parallel]
⇒ AEFD is parallelogram
⇒ AE = GP
But is the midpoint of AB
∴ AE = BE
⇒ GP = PH
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
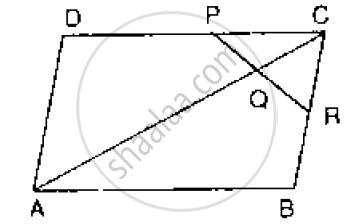
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

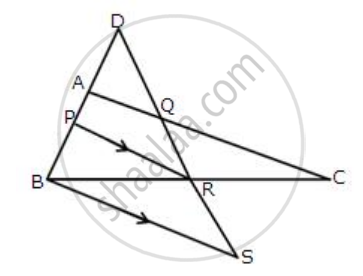
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm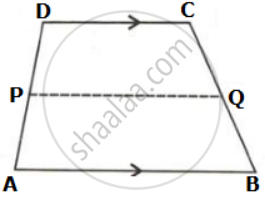
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
