Advertisements
Advertisements
प्रश्न
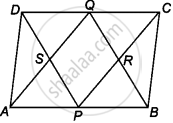
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
उत्तर
Given: In a parallelogram ABCD, P and Q are the mid-points of AS and CD, respectively.
To show: PRQS is a parallelogram.
Proof: Since, ABCD is a parallelogram.
AB || CD
⇒ AP || QC
Also, AB = DC
`1/2`AB = `1/2`DC ...[Dividing both sides by 2]
⇒ AP = QC ...[Since, P and Q are the mid-points of AB and DC]
Now, AP || QC and AP = QC
Thus, APCQ is a parallelogram.
∴ AQ || PC or SQ || PR ...(i)
Again, AB || DC or BP || DQ
Also, AB = DC
⇒ `1/2`AB = `1/2`DC ...[Dividing both sides by 2]
⇒ BP = QD ...[Since, P and Q are the mid-points of AB and DC]
Now, BP || QD and BP = QD
So, BPDQ is a parallelogram.
∴ PD || BQ or PS || QR ...(ii)
From equations (i) and (ii),
SQ || RP and PS || QR
So, PRQS is a parallelogram.
Hence proved.
APPEARS IN
संबंधित प्रश्न
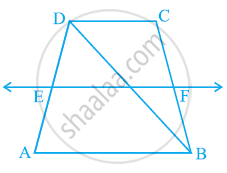
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
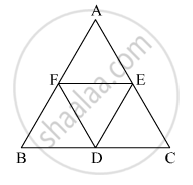
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.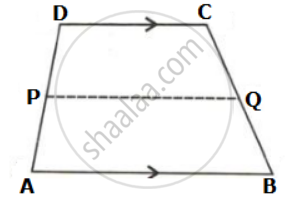
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
